Análisis Compositivo II

La enciclopedia colaborativa de Análisis Compositivo II

Relaciones de similitud [Editar]

  Las relaciones de similitud son formuladas por Allen Forte para comparar dos y no más conjunto de clases de altura o pc-sets que no son equivalentes y que comparten una misma cardinalidad. Hay diferentes grados de similitud entre dos pc-set y los aspectos centrales a tener en cuenta para su comparación son el contenido interválico y la relación de inclusión.

Forte propone cuatro tipos de relaciones entre pc sets de igual cardinal:

Rp: Similitud máxima en relación a las clases de alturas Es cuando dos pc sets de n-cardinalidad comparten un mismo subgrupo de cardinalidad n-1. Presenta algunas desventajas, un pc set puede relacionarse con muchísimos otros pc sets de acuerdo a este tipo de relación, sin posibilidad de particularizar nuestras observaciones. Por ejemplo, el pc set 4-2 está en relación rp con los pc-set 4-1, 4-3, 4-4, 4-6, 4-7, 4-10, 4-11, etc. Para dar cuenta de este problema, Forte nos dice que fijemos nuestra mirada en la similitud dada por el contenido interválico, es decir, en la correspondencia entre los ic de cada vector interválico. Si dos pc-sets poseen cuatro clases de intervalos idénticos, Forte denomina esta relación como máximamente similar. Esta similitud en referencia al vector interválico abarca dos tipos de relaciones: R1 y R2.

R1: similitud máxima en relación a la clase de intervalo y cuando los ic que no corresponden pueden intercambiarse para que todas las ic sean similares entre los dos pc-sets

              

 R2: similitud máxima en relación a la clase de intervalo. Sin característica de intercambio.

              

En el ejemplo, si se comparan los vectores interválicos, cuatro de las 6 entradas coinciden, sin embargo las dos restantes no pueden intercambiarse como ocurría en el ejemplo anterior. 

Por último, si en el vector interválico no hay correspondencia entre vectores la relación será minimamente similar (R0).

 

Aclaraciones de Forte:

La similitud Rp sólo cobra significado cuando está combinada con las relaciones que toman en cuenta los ic (R1 o R2). A partir de esto podemos apreciar distintas combinaciones entre los cuatro tipos de relaciones.

Ej: 4-2 está en relación Rp y R1 con 4-3 y 4-22 

En cambio si tuviéramos en cuenta solo Rp: 4-2 estaría en relación con 4-1, 4-3, 4-4, etc.

 En el ejemplo se puede observar que 4-2 y 4-3 comparten el tricordio 0,1,4 y cuatro ic, siendo las dos restantes intercambiables. Y por otro lado 4-2 y 4-22 comparten el tricordio 0,2,4 y también cuatro ic idénticas y dos intercambiables.

 

Tablas de Forte:

 Forte elaboró una serie de tablas para poder visualizar fácilmente todas las relaciones entre los distintos pares de pc-sets de cardinalidad 4, 5 y 6.

Esta tabla pertenece a las relaciones R2 y Rp de los pc-sets de cardinalidad 4, a cada pc-set le corresponde una fila y una columna, y cada número de la tabla pertenece al ordinal del nombre del pc-set. De esta manera se visualizan rápidamente cada una de las relaciones.

Réplicas de Charles Lord hacia las relaciones de similitud formuladas por Forte: [Editar]

 Charles Lord, en el capítulo “Relaciones de Similitud interválica en el Análisis de Grupos de Clases de Alturas de la Música Atonal”, declara su disconformidad hacia los resultados obtenidos en los análisis que implementan las “Relaciones R” propuestas por Forte, tanto en términos de su precisión como de su importancia musical. Lord señala que aparecen varios problemas en su aplicación:

 Por un lado, la nomenclatura de las relaciones de similitud interválica parece ilógica, si R0 representa la menor similitud, R1 no debería designar una relación más fuerte que R2. Por otro lado, estas relaciones no cubren todas las posibilidades, Lord asegura que algunos grupos pueden ser considerados como menos que la relación máxima, pero más que la relación mínima, de manera que la medida de similitud demanda una escala de valores  relativos, no señalados por Forte.

 En vista de estos problemas Lord propone una función de similitud (sf) que ofrece algunas ventajas, propone la siguiente fórmula:

 "Para cualquier par de pc set X e Y de la misma cardinalidad, la función de similitud es igual a la mitad de la suma de los valores absolutos de las diferencias entre las correspondientes entradas de cada vector."

Como resultado podemos señalar algunas ventajas. Por un lado, mientras que antes teníamos pares de pc set que no aparecen en las relaciones R reseñadas por Forte, la sf asigna un valor para cada par. Por otro lado, los valores asignados son cuantitativos, lo cual nos da mayor información de la que ofrecen las relaciones de Forte.

 Si tenemos dos vectores interválicos que corresponden a un par de pc-sets de igual cardinalidad podemos rápidamente comparar la relación existente entre ellos a través del procedimiento propuesto por Lord. Por ejemplo:

Nombre: 5-2    pcs: 0,1,2,3,5  vector: 332110

Nombre: 5-11  pcs: 0,2,3,4,7  vector: 222220

La operación se realiza de la siguiente manera:

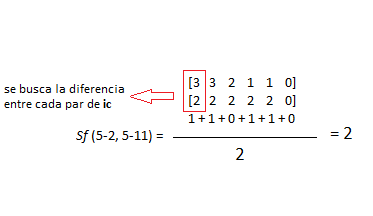
En este caso la relación sería de 2, cuánto menor es el número mayor es el grado de similitud entre los pc-sets.

 Para concluir, podemos ver con claridad las ventajas que surgen a partir del método propuesto por Lord, ya que funciona, a nivel intuitivo, mucho mejor que las relaciones R de Forte. Por otro lado, hay algunas relaciones que no pueden ser visualizadas por el método de Forte, Lord contribuye en ese sentido brindando una imagen más completa y específica de la similitud interválica de los pc-sets. 

 

Bibliografía: [Editar]

 Forte. Allen. The Structure of atonal music, New Haven & London: Yale University Press (1973); “Appendix I. Primer Forms and Vectors of Pitch-Class Sets”, pp. 179-181; “Appendix II. Similarity Relations”, pp. 191-198.

Sammartino, Federico. “Traducción y Resumen (aunque no tanto), del texto de Allen Forte The Structure of Atonal Music” (New Haven and London: Yale University Press, 1973), Apunte de cátedra (2012).

Lord, Charles H. "Intervallic Similarity Relations in Atonal Set Analysis", en Journal of Music Theory, Vol. 25, No. 1 (1981), pp. 91-111 (Trad. F. Sammartino).