Wiki de Análisis II

La enciclopedia colaborativa de Análisis Compositivo II
Versión imprimible

Forma Prima

Tabla de contenidos

1. Utilidad e importancia de la forma prima [Editar]

2. Método para la obtención de la forma prima [Editar]

Dentro de la Set Theory, el término forma prima se refiere a la forma mas compacta de una clase de alturas, comenzando por la nota 0 -en cero variable- entendiendo como forma más compacta aquella que dispone dentro de un pc set dado las alturas de manera tal que la distancia interválica entre la primer nota y la última sea la menor, luego de comparar todas las permutaciones circulares posibles.

Utilidad e importancia de la forma prima [Editar]

Todos los sets derivados uno de otros sea por transposición y/o inversión derivan de una misma forma prima. Por lo tanto, la forma prima resulta de extrema utilidad al mostrar la equivalencia entre pc-sets de la misma cardinalidad. Dos pc sets serán equivalentes sí y sólo sí pueden reducirse a la misma forma prima por transposición o por inversión seguida de transposición.

Allen Forte catalogó cada forma prima posible de sets con 3 a 9 miembros y las ordenó según su contenido interválico. Le dio a cada una un nombre (p.ej 5-35) indicando el primer número cuantas alturas hay presentes en el set.

Método para la obtención de la forma prima [Editar]

Existen diversos métodos para la obtención de la forma prima. A continuación se detallan los pasos para obtener la forma prima utilizando la notación hexadecimal, para mayor velocidad. Tomaremos como ejemplo el siguiente PC set:

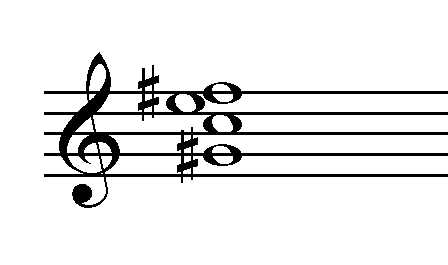
Se escriben las clases alturas en orden ascendente de menor a mayor. No debe existir ninguna clase de altura duplicada.

 

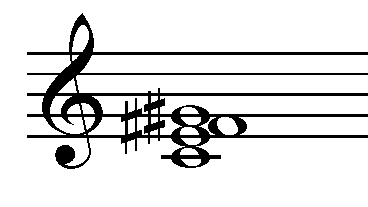
Se listan todas las permutaciones circulares posibles. Se ubica el primer número al final y se le suma 12.

       [0,4,6,8]        [4,6,8,12]     [6,8,12,16]   [8,12,16,18]

Entonces las permutaciones circulares posibles del pc set ejemplo son:
[0,4,6,8]
[4,6,8,12]
[6,8,12,16]
[8,12,16,18]

Se determina cuál de las permutaciones del PC set posee la menor distancia entre el primer y el último elemento

[0,4,6,8]  8-0 = 8
[4,6,8,12]  12-4 = 8
[6,8,12,16]  16-6 = 10
[8,12,16,18]  18-8 = 10 
Tanto la permutación [0,4,6,8] como [4,6,8,12] poseen la menor diferencia entre el primer y el último elemento. Por lo que para saber cual es la adecuada debemos pasar al siguiente punto 

Si hay dos que poseen la misma distancia entre dichos elementos, se elije aquella permutación que tenga la menor distancia entre el primer y el segundo número


[0,4,6,8]  4-0 = 4
[4,6,8,12]  6-4 = 2

Entonces en nuestro ejemplo vemos que la permutación más compacta es [4,6,8,12] , o lo que se denomina orden normal

En caso de que aún existan dos permutaciones que posean la misma distancia entre el primer y segundo elemento, se toma la menor distancia entre el primer y tercer elemento.
Transponemos el Pc set de manera que el primer número sea cero (notación del cero variable). Para ello restamos a todos los elementos el valor del primer elemento, si el resultado es negativo le sumamos 12

[4,6,8,12]

4-4 = 0
6-4= 2
8-4= 4

12-4= 8

Entonces la forma prima nuestro Pc set es: [0,2,4,8]


  1. Podemos buscar en la tabla de Forte el “Forte Name” para catalogar la forma prima. En dicha tabla encontraremos las 216 formas primas posibles.

    para nuestro Pc set en particular, el “Número de Forte” sería 4-24 (12)

 

  1. Ocasionalmente encontraremos que la forma prima que obtenemos no se encuentra en la tabla de Forte. En este caso lo que debemos hacer es invertir el pc set.

    Por ejemplo si obtuvimos la forma prima [0,3,4,8]