Análisis Compositivo II

Números entre paréntesis “”

Los números entre paréntesis son utilizados por Allen Forte en su “Análisis proporcional de las duraciones” para representar unidades de longitud correspondientes a particiones ataque-final o simplemente particiones. Estas particiones son segmentaciones tonales, en ataques y finales de sonido, de un pasaje de música. Forte expresa que las particiones ataque-final  deberían ser consideradas más precisamente como patrones de ataques o patrones rítmicos. Estas particiones dividen la duración total de una unidad musical en celdas de longitud específica. Recordamos que las particiones ataque-final  cumplen una función musical muy importante al articular componentes de altura, dando forma a las estructuras de subconjunto, coordinando elementos de conjuntos (sets) traslapados o intersectados y, en general, controlando su interacción y modo de presentación en la composición global de la música. Los silencios en la música, que son representados  por las líneas quebradas, son importantes para las particiones ataque-final  y para las estructuras que ellas forman con el avance de la música. La duración de un silencio es representada también por la cantidad de valores correspondientes a la figura que posee la menor duración absoluta del pasaje.

Algunas de las unidades de longitud más importantes representadas entre paréntesis son: la unidad duracional básica y la unidad básica de ataque. Podemos observar en la Bagatela n°5 Op.9 de Webern  como estas dos unidades son representadas por un mismo valor en el comienzo de la pieza.  Aquí el gráfico proporcional  realizado por Forte  sobre los primeros compases:

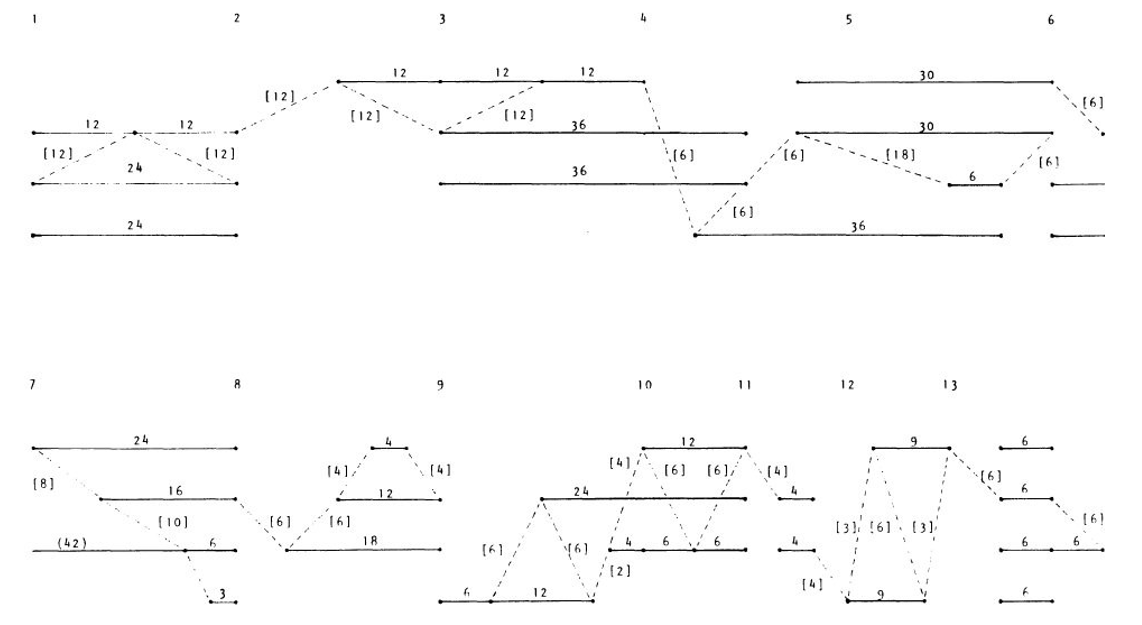
Podemos observar que una longitud 24 (c.1) está particionada por el ataque-final de un instrumento dando como resultado dos unidades de longitud 12 cada una. Estas particiones son representadas como bien habíamos dicho, entre paréntesis, (12) (12). Forte denomina a esto proportio dupla como a la relación que hay entre la longitud 48, que comienza con el ataque del violín 1 en c.2 y finaliza en c. 4 con violín 2 y viola, y la  longitud 24 del fragmento de apertura. 48 es el doble y su partición correspondiente a las formaciones duracionales que la integran  es (12) (12) (12) (6) (6); (6) es la mitad de la unidad duracional básica 12 por lo que, he también aquí, se establece una proportio dupla. Otros tipos de relaciones, presentes en el pasaje, de proporción a causa de las particiones, son la sesquialtera - (6) (6) (18) (6) de la longitud 36 del violonchelo, c.4 a c.6, junto con la unidad duracional básica forman la proporción 3/2 relacionada de manera orgánica con la proportio dupla  como se observa en (12) (6) (18) - , la tripla,  y otras. Un ejemplo de varias de estas proporciones operando de manera conjunta es en c.8 donde una longitud total 18 (viola) está particionada en (6) (12) por violín 2, y 12 es particionada por violín 1 en tres celdas de longitud 4 estableciendo como partición total a (6) (4) (4) (4). La proportio dupla se ve representada por (12) (6), la proportio sesquialtera por (6) (4) y la proportio tripla por (4) (4) (4).   Estas relaciones son presentadas por Allen Forte en una partición completa de ataques-finales:

Bibliografía

• Forte, Allen. “Aspects of Rhythm in Webern’s Atonal Music”, Music Theory Spectrum, 2 (1980). “Aspectos del ritmo en la música atonal de Webern”. pp 90-109 (Trad. César de Madeiros)